近日,理学院数学系教师李林林在应用数学领域取得进展,相关成果以“Time periodic reaction-diffusion equations in funnel-shaped domains”为题,发表于数学领域期刊Journal of Differential Equation。
在自然界与工程实际中,许多系统的空间结构是非均匀的,并且系统中可能会存在随时间周期性变化的反应,该研究聚焦于一端为直圆柱、另一端为扩张圆锥的“漏斗形”域,能更真实地模拟许多物理、生物系统中物质的变化情况。
本研究通过构造在时间周期与空间变截面的非均匀条件下的整体解,建立完全传播(Complete Propagation)与传播阻塞(Blocking)的判别准则:当漏斗入口(圆柱部分)半径R足够大,且扩张角α在一定范围内时,来自左侧的周期性波能够完全传播。而当漏斗入口半径R足够小,扩张角α非常大时,波会被阻塞。
这些研究成果不仅具有理论价值,在其他应用领域也具有实际指导意义。例如在环境科学中,污染物或化学物质在变截面河道或地下水层中的扩散与反应过程,可借助该模型评估其在空间非均匀结构中的传播行为等。
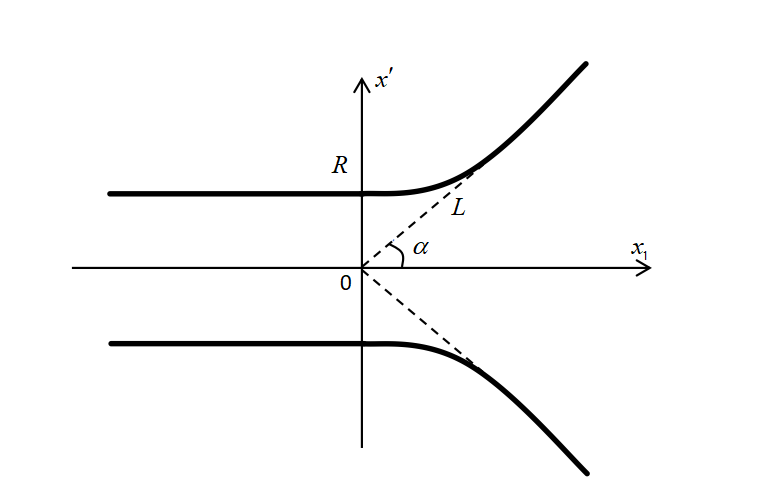
漏斗形区域的截面图
论文链接:https://www.sciencedirect.com/science/article/abs/pii/S0022039625007090



